Research ArticleBasic Science Investigation

A Deep-Learning–Based Partial-Volume Correction Method for Quantitative 177Lu SPECT/CT Imaging

Julian Leube, Johan Gustafsson, Michael Lassmann, Maikol Salas-Ramirez and Johannes Tran-Gia
Journal of Nuclear Medicine June 2024, 65 (6) 980-987; DOI: https://doi.org/10.2967/jnumed.123.266889

Abstract

With the development of new radiopharmaceutical therapies, quantitative SPECT/CT has progressively emerged as a crucial tool for dosimetry. One major obstacle of SPECT is its poor resolution, which results in blurring of the activity distribution. Especially for small objects, this so-called partial-volume effect limits the accuracy of activity quantification. Numerous methods for partial-volume correction (PVC) have been proposed, but most methods have the disadvantage of assuming a spatially invariant resolution of the imaging system, which does not hold for SPECT. Furthermore, most methods require a segmentation based on anatomic information. Methods: We introduce DL-PVC, a methodology for PVC of 177Lu SPECT/CT imaging using deep learning (DL). Training was based on a dataset of 10,000 random activity distributions placed in extended cardiac–torso body phantoms. Realistic SPECT acquisitions were created using the SIMIND Monte Carlo simulation program. SPECT reconstructions without and with resolution modeling were performed using the CASToR and STIR reconstruction software, respectively. The pairs of ground-truth activity distributions and simulated SPECT images were used for training various U-Nets. Quantitative analysis of the performance of these U-Nets was based on metrics such as the structural similarity index measure or normalized root-mean-square error, but also on volume activity accuracy, a new metric that describes the fraction of voxels in which the determined activity concentration deviates from the true activity concentration by less than a certain margin. On the basis of this analysis, the optimal parameters for normalization, input size, and network architecture were identified. Results: Our simulation-based analysis revealed that DL-PVC (0.95/7.8%/35.8% for structural similarity index measure/normalized root-mean-square error/volume activity accuracy) outperforms SPECT without PVC (0.89/10.4%/12.1%) and after iterative Yang PVC (0.94/8.6%/15.1%). Additionally, we validated DL-PVC on 177Lu SPECT/CT measurements of 3-dimensionally printed phantoms of different geometries. Although DL-PVC showed activity recovery similar to that of the iterative Yang method, no segmentation was required. In addition, DL-PVC was able to correct other image artifacts such as Gibbs ringing, making it clearly superior at the voxel level. Conclusion: In this work, we demonstrate the added value of DL-PVC for quantitative 177Lu SPECT/CT. Our analysis validates the functionality of DL-PVC and paves the way for future deployment on clinical image data.

Quantitative SPECT/CT has become the method of choice to spatially resolve activity distributions for the dosimetry of radiopharmaceutical therapies. One of the most important radionuclides used today is 177Lu (1,2). Mainly because of its nonperfect collimation and the resulting relatively poor spatial resolution (1–2 cm for 177Lu and medium-energy collimation (3)), 177Lu SPECT imaging reaches its limitations for small structures such as lesions or small organs (4). When activity quantification is based on volumes of interest, poor spatial resolution leads to spatial allocation uncertainty, which is referred to as partial-volume effect. For many imaging modalities, the acquired activity distribution can be described in good approximation by a convolution of the true activity distribution with the point-spread function of the imaging system. Since this approximation holds for PET, several techniques for partial-volume correction (PVC) of PET have been proposed (5). However, the fundamental problem for transferring such methodology to SPECT is that the poor spatial resolution of gamma cameras inevitably leads to information loss. Hence, purely data-driven methods, such as resolution modeling during reconstruction (resolution recovery [RR]) (6) or postreconstruction deconvolution, will never result in partial-volume effect–free activity concentration estimates. Accordingly, some form of prior information has to be supplied, as performed, for example, in the iterative Yang technique for postreconstruction PVC (5), an enhancement of the Yang method (7). Iterative Yang PVC (IY-PVC) uses prior knowledge about the spatial resolution to fold the activity back into an estimated mask of active volume. For practical implementation of PVC methods, a spatially invariant point-spread function is often assumed for the sake of simplicity, which approximately holds true for PET imaging. For SPECT, however, this may introduce substantial errors, as the spatially variant SPECT resolution cannot be well approximated by a single value (3). Furthermore, the exact distribution of radiopharmaceuticals in the structures under investigation is typically unknown and can be only roughly estimated from morphologic imaging such as CT. When the active regions cannot be properly defined on the basis of morphologic imaging, substantial errors may be introduced.

In recent years, convolutional neural networks have demonstrated their tremendous potential in medical image processing. In the field of SPECT imaging, convolutional neural networks have been used for automated segmentation (8), CT-free attenuation correction (9), acceleration of SPECT imaging (10,11), and denoising (12). In addition, deep learning (DL) techniques have recently been used for PVC (13,14). Xie et al. (13) trained a neural network to perform IY-PVC without the need for segmentation using uncorrected SPECT images as input and images corrected with IY-PVC as target. As mentioned above, however, the prior knowledge used to train the network can introduce systematic errors. Li et al. (14) proposed a DL-based enhancement of dose calculations. More specifically, they used [68Ga]Ga-DOTATATE PET/CT patient data as ground truth to reduce the partial-volume effect in [177Lu]Lu-DOTATATE SPECT/CT–based absorbed dose distributions. Although the method was shown to enhance the dose maps, it works only under the assumption that the distribution of radiopharmaceutical is comparable despite the different radiopharmaceuticals scanned at different measurement times after administration. In addition, differences in ligand amount, affinity, and internalization have not yet been sufficiently investigated, possibly leading to additional errors (15). Both studies, although demonstrating the potential of DL for PVC, suffer, like many other published implementations of DL for clinical applications, from small dataset sizes (28 and 14 patients in the work of Xie et al. (13) and Li et al. (14), respectively) and lack of ground-truth activity distributions for training.

In this work, we present DL-PVC, a methodology for PVC of 177Lu SPECT/CT imaging using DL trained on a large dataset of 10,000 pairs of random patient-shaped activity distributions and associated SPECT images generated using Monte Carlo radiation transport simulations. These pairs are used as input and target for a convolutional neural network, trained to perform PVC without segmentation. For performance evaluation, we investigated the impact of different normalization (i.e., activity conservation) methods, input matrix sizes, and network architectures on the performance of DL-PVC. Subsequently, we compared our new methodology with IY-PVC as a reference method and performed a validation based on 177Lu SPECT/CT measurements of 3-dimensionally printed phantoms of different geometries.

MATERIALS AND METHODS

Generation of a Dataset of Random Activity Distributions

A large database of 3-dimensional activity distributions of randomly arranged random shapes and corresponding SPECT simulations was created to train neural networks for PVC. A schematic overview of the dataset generation is given in Figure 1. First, density maps and activity masks were generated. The activity masks were then transformed into inhomogeneous activity distributions with a patientlike activity range. Next, simulations were performed in the SIMIND (SImulating Medical Imaging Nuclear Detectors) Monte Carlo simulation program (16), using these masks to obtain SPECT projections. Last, iterative reconstructions with RR (Software for Tomographic Image Reconstruction, STIR (17)) and without RR (Customizable and Advanced Software for Tomographic Reconstruction, CASToR (18)) were performed to obtain SPECT images. The approach is based on previously described work (11). A detailed description of the generation of the dataset is given in the supplemental materials (supplemental materials are available at http://jnm.snmjournals.org). In addition, the complete dataset is available at https://doi.org/10.5281/zenodo.8282567.

FIGURE 1.
FIGURE 1.

Schematic overview of dataset generation used in this study. SIMIND = Simulating Medical Imaging Nuclear Detectors. STIR = Software for Tomographic Image Reconstruction; CASToR = Customizable and Advanced Software for Tomographic Reconstruction.

The most important features of the dataset are as follows:

Realistic Attenuation and Scattering Conditions

Extended cardiac–torso (XCAT) phantoms (19) were used to achieve realistic attenuation and scatter conditions. By varying the size scaling of individual organs or areas, 250 variations of 16 patients (6 female, 9 male; age, 18–76 y; body mass index, 18.6–38.0) resulted in a total of 4,000 different density maps. By defining 3 bed positions, we generated a total of 10,000 attenuation images (4,000 thoracic, 4,000 abdominal, and 2,000 head images; matrix, 256; voxel size, 2.4 mm).

Patientlike Binary Activity Masks

Patientlike binary activity masks (0, no activity; 1, activity) were created by placing random shapes (minimal and maximum shape sizes of 4 and 100 voxels, respectively), created using previously described methodology (11), inside the XCAT-based attenuation mask until a randomly selected, patient-representative target volume was reached.

Nonuniform Activity Distributions

Each activity mask was multiplied voxelwise by a spatially contiguous, nonuniform pattern (11) to create more complex, heterogeneous activity distributions. An example of the resulting target datasets used to train the neural network is shown in Figure 2.

FIGURE 2.
FIGURE 2.

Example target dataset as used for neural network. XCAT phantom is shown in gray scale, whereas random activity distribution is shown in color map. At top are axial sections, and at bottom are coronal sections. From left to right, 3 bed positions are shown: head, thorax, and abdomen. Camera orbits are indicated as blue dotted lines.

Realistic Activity Distributions

To resemble 177Lu SPECT patient acquisitions as closely as possible, the activity distributions were scaled on the basis of the active volumes and total activities of 717 peritherapeutic 177Lu SPECT/CT acquisitions (429 [177Lu]Lu-PSMA-I&T and 288 [177Lu]Lu-DOTATATE SPECT/CT examinations of 202 different patients), which had been conducted at University Hospital Würzburg between January 2014 and June 2021 (waiver 20230207 04).

Monte Carlo–Based SPECT Simulations

For each of the 10,000 random activity distributions, a set of realistic SPECT projections was generated by SIMIND Monte Carlo simulations (16). The simulations were set up to replicate a 177Lu SPECT acquisition on our Siemens Intevo Bold SPECT/CT system (9.5-mm crystal; medium-energy low-penetration collimator; 9% energy resolution; 120 projections of 30 s each; noncircular orbit; matrix, 128; pixel size, 4.79 mm; 20% main energy window at 208 keV; and 2 adjacent 10% scatter windows). As described previously (11), Poisson noise was added to the simulated (noise-free) projections to obtain realistic (noisy) projections for the given activities and acquisition parameters.

SPECT Reconstructions

SPECT reconstructions (voxel size, 4.8 mm) were performed for all 2 × 10,000 projection sets (noise-free and noisy) using 2 different reconstructions: CASToR, an ordered-subset expectation maximization reconstruction (10 iterations, 2 subsets, attenuation correction, scatter correction) without RR (18), and STIR, an ordered-subset expectation maximization reconstruction (6 iterations, 6 subsets, attenuation correction, scatter correction) with RR (17). Accordingly, 4 different SPECT datasets were available for training and analysis of the presented approach: CASToR (noRR) or STIR (RR) performed with noise-free (nf) or noisy (n) projections (noRR_nf/noRR_n and RR_nf/RR_n, respectively).

Evaluation of Activity Conservation

An important criterion for any PVC is that the correction preserves the total activity. Before the U-Net was applied, the input SPECT images were normalized by their maximum activity concentration to an interval of [0,1]. In this study, we investigated 2 different approaches for scaling the output of the proposed PVC. The first was rescaling the output of DL-PVC with the maximum activity concentration of the input SPECT image, and the second was normalization of the sum of all voxel values of the output of DL-PVC to the total activity of the input SPECT image.

Evaluation of Input Matrix Size

In our work, we investigated 2 kernel sizes to which the PVC method was applied. In the first, DL-PVC is directly applied to the entire field of view (FOV), in which case the entire SPECT image (matrix size, 128 × 128 × 128) and the entire ground-truth activity distribution serve as input and target, respectively. In the second, DL-PVC is applied to smaller patches (cube-shaped image sections with an edge length of 32 voxels), which are subsequently reassembled (more details can be found in the supplemental materials).

Evaluation of U-Net Architecture

A 3-dimensional U-shaped convolutional neural network (U-Net) (20) based on the fastMRI architecture (21) and implemented using the PyTorch library (22) with Adam optimizer (23) was used to perform the PVC. A more detailed explanation of the architecture is given in the supplemental materials. In addition to the standard U-Net architecture, 4 other architectures were tested: R2U-Net by Alom et al. (24); AttU-Net by Oktay et al. (25); R2AttU-Net, a combination of both methods (26); and U-Net++, a nested U-Net proposed by Zhou et al. (27). The performance of these 5 network architectures was compared on the basis of the RR_n and noRR_n datasets. PVC was performed on the entire FOV, preserving the total activity.

Evaluation Criteria for PVC Performance

Several evaluation metrics were used to evaluate the quality of the different PVC methods. Their calculation was restricted to a masked region within each test dataset in which ground-truth activity was present. Besides structural similarity index measure (SSIM) (28) and normalized root-mean-square error (NRMSE), a volume activity accuracy (VAA) was defined. It indicates the proportion of voxels in which the relative deviation in activity concentration was less than α (fixed at 5%). More information is given in the supplemental materials. In addition, the deviation between total activity before and after PVC was calculated as percentage difference. Because not all evaluation metrics were normally distributed, paired Wilcoxon tests with a significance level of 1% were chosen for the statistical analysis.

Comparison with Iterative Yang Technique

To compare the proposed DL-PVC methodology with an already-established PVC method, IY-PVC (5) was applied to all SPECT reconstructions. First, a matched filter analysis (3) was used to determine the spatial resolution for STIR (8.75 mm; applies to RR_n, RR_nf) and for CASToR (21.35 mm; applies to noRR_n, noRR_nf). Subsequently, 10 iterations of IY-PVC were performed using the PETPVC toolbox (29) with spatial resolution and ground-truth activity mask as input.

Investigation of Minimum Feature Size

To determine the minimum feature size that DL-PVC can still resolve, further simulations based on the XCAT phantom dataset were performed. For this purpose, multiple SPECT simulations of random activity distributions were performed, in which a cube with an edge length of 1–10 voxels (increment, 1 voxel) was introduced centrally into the activity distribution. Recovery coefficients (RCs) were calculated to determine how well DL-PVC recovers the activity in the different-sized cubes. More detail on the simulations and the calculation of the RCs is given in the supplemental materials.

Activity Concentration–Voxel Histograms

To illustrate differences in the distribution of activity concentrations for the SPECT simulations without PVC, after IY-PVC, and after DL-PVC, activity concentration–voxel histograms (proportion of voxels containing a given relative activity concentration plotted against the respective relative activity concentration) were created. More details can be found in the supplemental materials.

Phantom Measurement

To justify application of DL-PVC in a clinical context, we validated the methodology on increasingly patient-realistic 177Lu SPECT/CT phantom measurements. For this purpose, a previously published series of 177Lu SPECT/CT measurements of 3 self-designed 3-dimensional phantoms (sphere, ellipsoid, and renal cortex geometry, all with the same filling volume of 100 mL) was used (30). In addition, a 3-dimensionally printed 2-organ phantom (International Commission on Radiological Protection publication 110 [ICRP110]–based 2-compartment kidney and spleen) was analyzed to evaluate DL-PVC on a phantom that is more representative of patient data. These data had been acquired at our institution as part of the Europe-wide MRTDosimetry comparison exercise for quantitative 177Lu SPECT/CT imaging (31). The acquisition parameters had been the same as the parameters chosen for the Monte Carlo simulations. On the basis of these 4 measured projection datasets, SPECT reconstructions were performed with CASToR and STIR with the same parameters as for the simulated SPECT projections. For analysis, all SPECT images were interpolated to CT resolution (matrix, 512; voxel size, 0.98 mm) using trilinear interpolation. These were compared with the ground truth created by multiplying the masks used for phantom fabrication by the nominal activity concentrations (1.08 ± 0.03 MBq/mL for sphere/ellipsoid/cortex, 1.44 ± 0.04 MBq/mL for spleen/cortex, and 0.47 ± 0.01 MBq/mL for medulla of the ICRP110-based phantom), the determination of which was previously described (30).

RESULTS

Optimal Selection of Activity Conservation, Input Matrix Size, U-Net Architecture, and Resolution Modeling

In light of the investigations regarding activity conservation, input matrix size, U-Net architecture (20,24–27), and the application of RR, an optimal configuration and reconstruction method, DL-PVC, was determined for further analysis. It comprises the following components, the selection of which, including statistical tests based on the evaluation metrics, are described in detail in the supplemental materials: SPECT reconstruction with RR (RR_nf or RR_n); activity conservation based on the total activity of the uncorrected SPECT; input matrix size: direct application of PVC to the entire FOV; and R2U-Net network architecture (24).

Comparison with Iterative Yang Technique as Reference Method

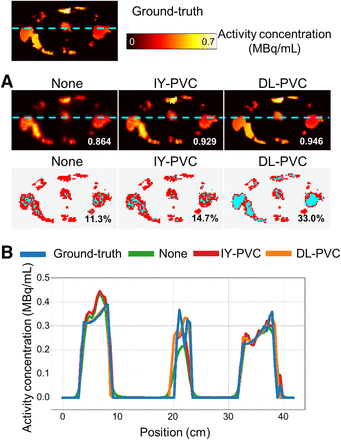
Table 1 and Figure 3 show a numeric and visual comparison of the evaluation metrics for SPECT without PVC, after DL-PVC, and after IY-PVC. In both cases, DL-PVC demonstrates significantly superior evaluation metrics. In addition, Figure 4 gives a visual impression of the different image qualities. Visually, activity distributions corrected with DL-PVC closely resemble the ground-truth activity distribution, which is illustrated by cross sections. A considerable increase in the number of cyan voxels in the VAA maps indicates that the activity concentration after DL-PVC better matches the true activity concentration. Furthermore, the true activity concentration is restored, especially in voxels located at the center of larger shapes. However, deviations can still be seen at the edges of larger objects or for smaller objects.

View this table:
TABLE 1.

Mean Evaluation Metrics for Both SPECT Datasets with RR Without PVC, After IY-PVC, and After DL-PVC over All 500 Test Activity Distributions

FIGURE 3.
FIGURE 3.

Comparison of different PVC approaches. Depicted are violin plots of evaluation metrics for SSIM (A), NRMSE (B), VAA (C), and activity deviation (D) for reconstructions without PVC, after IY-PVC, and after DL-PVC. Darker shades represent reconstructions without RR, and brighter shades represent reconstructions with RR. Inside violins, solid lines represent median, and dashed lines represent upper and lower quartiles. Note that activity deviation is same without PVC and after DL-PVC because of activity conservation in DL-PVC. For SSIM and VAA, higher values correspond to better performance, whereas for NRMSE and activity deviation, better performance is indicated by values closer to 0%. AD = activity deviation; NRMSE = normalized root-mean-square error; SSIM = structural similarity index measure; VAA = voxel activity accuracy.

FIGURE 4.
FIGURE 4.

Visual performance analysis of different PVC approaches. (A) Top: axial slice of example activity distribution from test dataset reconstructed with RR without PVC, after IY-PVC, and after DL-PVC. White numbers correspond to SSIM values with respect to ground truth. Bottom: VAA maps of corresponding SPECT reconstructions with respect to ground truth. Red represents deviation in voxel’s activity concentration by more than or equal to Embedded Image; cyan represents deviation smaller thanEmbedded Image. Black numbers indicate VAA between SPECT reconstruction and ground truth. (B) Cross-sections indicated by cyan lines in SPECT reconstructions in A. SSIM = structural similarity index measure; VAA = voxel activity accuracy.

Investigation of Minimum Feature Size

Figure 5 shows the results concerning the minimal feature size that DL-PVC can resolve. Without PVC (green) and after IY-PVC (red), the RCs increase continuously over all cube edge lengths investigated. In contrast, the RCs for DL-PVC are zero at edge lengths of 1 and 2 voxels (4.8 and 9.6 mm), increase rapidly from an edge length of 3 voxels (14.4 mm), and then continue to increase only slowly. Although DL-PVC does not perform adequately for structures with an edge length of less than 3 voxels (14.4 mm), it outperforms no PVC or IY-PVC for all cubes above this resolution limit.

FIGURE 5.
FIGURE 5.

Investigation of minimum feature size. (Top) axial slices of reconstructed SPECT simulation without PVC, after IY-PVC, and after DL-PVC. (Center) RC as function of cube edge length. Dashed blue line corresponds to cube edge length in ground-truth image (bottom left).

Activity Concentration–Voxel Histograms

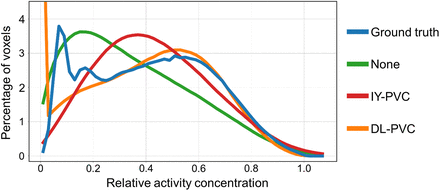
Figure 6 shows the activity concentration–volume histograms for the test dataset. For a perfect PVC, the histograms should closely resemble the ground-truth activity distribution. A close similarity between ground truth (blue) and DL-PVC (orange) can be observed at higher relative activity concentrations, starting at approximately 0.25. In general, substantial deviations can be seen for lower concentrations. Although, in the ground-truth activity distribution, a high proportion of voxels is associated with small concentrations between 0.05 and 0.25, the DL-PVC distribution has far fewer voxels in this concentration range. In contrast, there is a high fraction of voxels for DL-PVC in which no activity is present in comparison to the ground-truth activity distribution. This is due to the masking of the voxels displayed in the histogram based on the ground truth. The histograms of the SPECT reconstructions without PVC (green) and after IY-PVC (red) both show a distinct shift toward lower concentrations, indicating that DL-PVC outperforms IY-PVC on the voxel level.

FIGURE 6.
FIGURE 6.

Activity concentration–volume histograms for test dataset. Depicted are ground-truth activity distribution and corresponding SPECT reconstructions (RR_n) without PVC, after IY-PVC, and after DL-PVC. For better visualization, y-axis has been truncated at 4.5%; thus, high percentage of 7.2% of voxels at relative concentration of 0 for DL-PVC is not shown in plot.

Phantom Measurement

Table 2 shows the evaluation metrics for the phantom measurements. The results for the ellipsoid phantom are given in the supplemental materials, as they are quite similar to the sphere. For all 3 phantoms, the highest SSIM and lowest NRMSE were achieved using IY-PVC. Although DL-PVC results in worse SSIM and NRMSE, there is still a clear improvement. In contrast, the highest VAA was obtained using DL-PVC for all 3 phantoms. Although the best RCs for the sphere were achieved with DL-PVC, the highest recoveries for the kidney cortex and ICRP110 kidney/spleen were achieved by IY-PVC.

View this table:
TABLE 2.

Evaluation Metrics of Phantom Measurements for Reconstruction with RR (RR_n) Without PVC, After IY-PVC, and After DL-PVC

Figure 7 shows the results of the phantom measurements. In the activity distributions (Fig. 7A) and the corresponding cross sections (Fig. 7B), a good visual agreement between the true activity distribution (blue) and the SPECT reconstruction after DL-PVC (orange) can be observed for sphere and ellipsoid (supplemental materials) geometry. For the reconstruction without PVC (green) and with IY-PVC (red), an overestimation of the activity at the edges and underestimation centrally can be observed for the sphere phantom. This artifact, known as Gibbs ringing, disappears after the application of DL-PVC. The VAA maps (Fig. 7A) underline this good agreement. Similar to Figure 4, the voxels at the edge of the object deviate from the true activity distribution to a greater extent. For the kidney cortex, significant deviations are observed between the DL-PVC SPECT acquisition and the true activity distribution. The image appears blurred, and the narrow structure on the right could not be restored. Hardly any cyan voxels are visible in the VAA map, indicating that the true activity distribution was poorly reproduced numerically. However, IY-PVC also does not provide satisfactory results for this phantom geometry. For the ICRP110-based kidney/spleen phantom, DL-PVC cannot correctly predict the activity difference between the 2 compartments comprising the kidney. On the other hand, the voxelwise activity quantification in the spleen is significantly better than that for IY-PVC.

FIGURE 7.
FIGURE 7.

Phantom measurement. (A) SPECT reconstructions (RR_n) of 100-mL sphere phantom (axial slice), ICRP110-based kidney/spleen phantom (sagittal slice), and kidney cortex phantom (axial slice) without PVC, after IY-PVC, and after DL-PVC with corresponding VAA maps. Magenta arrow for cortex phantom indicates structure that could not be restored by DL-PVC. (B) Cross-sections indicated by cyan lines in SPECT reconstructions for ground-truth activity distributions and for SPECT without PVC, after IY-PVC, and after DL-PVC. (C) Corresponding activity concentration–voxel histograms; VAA = voxel activity accuracy.

The activity concentration–voxel histograms (Fig. 7C) show that for the sphere phantom and the ICRP110 kidney/spleen phantom, more voxels have the true activity concentration after DL-PVC than after IY-PVC. For the cortex phantom, the distribution of activity concentrations could at least be brought closer toward the true activity concentration.

DISCUSSION

In this work, we introduce a methodology for PVC of 177Lu SPECT/CT imaging using DL. Using a dataset consisting of random activity distributions and the corresponding SPECT simulations, a neural network was trained to estimate ground-truth activity distributions from SPECT images.

From simulated data and 177Lu phantom measurements, we demonstrated the superiority of the presented DL-PVC method over IY-PVC, an established method for PVC (5). This is despite the advantage that DL-PVC does not require any prior knowledge such as the spatial resolution of the reconstruction or a mask with the contours of the active volume. For spherelike geometries, DL-PVC achieved a recovery of the activity comparable to IY-PVC. However, Gibbs artifacts, which are typical for SPECT reconstructions with RR, and which were still clearly visible even after IY-PVC, could be efficiently corrected by DL-PVC. As a result, DL-PVC is clearly superior to IY-PVC in accurately restoring the true activity concentration at the voxel level, as is also reflected in the VAA. These artifacts could also be the reason why direct application of PVC to the entire FOV leads to a higher VAA than application of DL-PVC to smaller patches. For large objects, application of DL-PVC to smaller patches can no longer capture the entire object because of its 32 × 32 × 32 voxel kernel. Therefore, the neural network may be less capable of correcting Gibbs artifacts for larger objects, resulting in a smaller VAA. In contrast, IY-PVC proved to be superior in the case of the kidney cortex geometry, as could be attributed to its small features, some of which fall below the minimum resolvable feature size of 3 voxels (14.37 mm) determined for DL-PVC. However, only the cube geometry was used in the resolution analysis of the different PVC methods. Therefore, these conclusions may not apply in the same way to nonuniformly shaped objects. Another important aspect when comparing DL-PVC and IY-PVC is that the activity masks for our IY-PVC analysis were based on the ground-truth activity distributions, an approach that is not feasible under real clinical conditions. This represents a clear bias in favor of IY-PVC in the context of our quantitative analysis and may explain the better performance of IY-PVC for the cortex phantom, as the complex structure was precisely specified there in the form of the segmentation mask. For a fairer comparison, activity masks could additionally be used as prior knowledge to improve DL-PVC, which could be the subject of future research.

There are also other potential ways to further improve the performance of DL-PVC. A notable limitation of the method in its current implementation is the relatively coarse voxel size of 4.8 mm. A subdivision of the FOV captured by the detectors into smaller pixels—and thus voxels—would leave more degrees of freedom for the neural network, especially in the transition regions between activity and background. This could in turn improve the performance of DL-PVC, especially for objects with small feature sizes such as the cortex phantom. On the other hand, a smaller voxel size will lead to a reduced signal-to-noise ratio per voxel, which could negatively impact the performance of DL-PVC. Because of the extensive computational demands of higher-resolution simulations and the limited memory capacity of the graphics processing unit used for training the neural network, we opted for the coarser resolution (4.8 mm) in this work. In future research, DL-PVC could be adapted for smaller voxel sizes such as 2.4 mm.

Although XCAT phantoms realistically describe the attenuation in a patient, there are still clear differences between the random activity distributions used for training DL-PVC and those observed in SPECT/CT measurements in patients undergoing radiopharmaceutical therapy. To close this gap and enable the method to be applied to clinical patient data, PET/CT or SPECT/CT patient images could be used to generate synthetic activity distributions. In the case of SPECT, however, the strongly pronounced partial-volume effect would have to be considered. Another limitation of the dataset used for training DL-PVC is that the variation of activity concentration within the random shapes is of relatively low frequency, thereby not demonstrating any sharp edges. These missing examples during training could explain why the performance of DL-PVC for the 2-compartment kidney of the ICRP110-based phantom is not yet optimal.

Our investigations have demonstrated that DL-PVC performs significantly better for noise-free (RR_nf) than for noisy (RR_n) datasets. Therefore, another avenue for improving DL-PVC would be to apply the method to denoised SPECT reconstructions. However, obtaining virtually noise-free projections in SPECT measurements is not realistic in a clinical setting, particularly for acquisitions a few days after administration of the radiopharmaceutical. An alternative approach would be to first denoise the SPECT data (e.g., using a second neural network) and subsequently apply DL-PVC.

At last, DL-PVC might be enhanced by further optimizing the network architecture. Although we have benchmarked various end-to-end U-Net architectures in this study, the exploration of novel convolutional neural network architectures represents a potential pathway to further improve the performance of DL-PVC.

Despite the investigation of many aspects within the scope of this work, there are still several open questions. For example, the choice of parameters for reconstructing the input data for our neural network needs further investigation. In our study, fixed numbers of iterations and subsets were used for both reconstructions (CASToR, 10 iterations and 2 subsets; STIR, 6 iterations and 6 subsets). However, the impact of these parameters on SPECT-based activity distributions is well known. Higher numbers of updates (iterations × subsets) have been shown to enhance recovery substantially, though at the expense of increased image noise (3). To address this issue, future studies could focus on assessing the performance of DL-PVC as a function of the number of iterations.

Another important aspect is the total activity in the FOV of the SPECT image. We determined the total activity by analyzing patients who received [177Lu]Lu-PSMA-I&T or [177Lu]Lu-DOTATATE radiopharmaceutical therapy at our institution. The latest acquisitions had been performed 4 d after injection of the radiopharmaceutical. When SPECT/CT is performed at even later time points (32), it needs to be investigated how such low activities—and thus low signal-to-noise ratios—affect the performance of DL-PVC.

Finally, an important investigation before the clinical application of DL-PVC in radiopharmaceutical therapy dosimetry is its impact on dosimetry calculations. Only by dosimetric evaluations on various organs and tumors using different PVC methods could one see what improvements DL-PVC can offer not only in terms of simplification of dosimetry calculation but also in terms of its accuracy.

CONCLUSION

In this study, a DL-PVC methodology for PVC of 177Lu SPECT/CT imaging based on DL was introduced. Training of convolutional neural networks was based on a large dataset of Monte Carlo–simulated SPECT images of random activity distributions placed in different XCAT phantoms. From our investigations, we identified the optimal settings for DL-PVC in terms of activity conservation, input matrix size, and network architecture. Our analysis revealed that DL-PVC outperforms established PVC methods, such as IY-PVC, in restoring the true activity distribution without requiring resolution estimation or activity masking. Furthermore, tests on 177Lu SPECT/CT measurements of 3-dimensionally printed phantoms of different geometries showed that although DL-PVC and IY-PVC achieve equivalent levels of activity recovery, DL-PVC can also correct other image artifacts such as Gibbs ringing and is therefore clearly superior at the voxel level. In summary, we have demonstrated that DL offers a wide range of improvement opportunities for PVC of quantitative 177Lu SPECT/CT imaging. This is a first step toward a much-needed routine use of comparable techniques for dosimetry of radiopharmaceutical therapies.

DISCLOSURE

This study was funded by a grant from the German Research Foundation (Deutsche Forschungsgemeinschaft TR 1380/1-1) and partially by grants from the German Federal Ministry of Education and Research (13GW0357B), the Swedish Cancer Foundation (21 1754 Pj 01 H), and the Mrs. Berta Kamprad Foundation (FBKS 2019-44 and FBKS 2020-13). The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results. Michael Lassmann has received institutional grants from IPSEN Pharma, Nordic Nanovector, Novartis, and PentixaPharm. No other potential conflict of interest relevant to this article was reported.

KEY POINTS

QUESTION: Is it possible to perform PVC for 177Lu SPECT/CT using DL?

PERTINENT FINDINGS: From a database of 10,000 pairs of random activity distributions and realistic associated SPECT simulations, a U-shaped convolutional neural network was trained to perform PVC on 177Lu SPECT images. SPECT images corrected with DL-PVC were found to resemble the underlying activity distribution much more closely than reconstructions without PVC or after application of IY-PVC.

IMPLICATIONS FOR PATIENT CARE: The potential of DL-PVC was demonstrated on 177Lu SPECT/CT measurements of anthropomorphic phantoms, paving the way for clinical application. In the future, DL-based PVC could be an important tool to perform accurate patient-specific and voxel-based dosimetry for radiopharmaceutical therapies.

ACKNOWLEDGMENTS

We thank Andrew Marsh for help with the generation of the random shapes and Anna-Lena Theisen for segmentation of the phantoms.

Footnotes

  • Published online Apr. 18, 2024.

REFERENCES

  1. 1.↵
    1. Kratochwil C,
    2. Fendler WP,
    3. Eiber M,
    4. et al
    . Joint EANM/SNMMI procedure guideline for the use of 177Lu-labeled PSMA-targeted radioligand-therapy (177Lu-PSMA-RLT). Eur J Nucl Med Mol Imaging. 2023;50:2830–2845.
    OpenUrlCrossRef
  2. 2.↵
    1. Sjögreen Gleisner K,
    2. Chouin N,
    3. Gabina PM,
    4. et al
    . EANM dosimetry committee recommendations for dosimetry of 177Lu-labelled somatostatin-receptor- and PSMA-targeting ligands. Eur J Nucl Med Mol Imaging. 2022;49:1778–1809.
    OpenUrl
  3. 3.↵
    1. Tran-Gia J,
    2. Lassmann M
    . Characterization of noise and resolution for quantitative 177Lu SPECT/CT with xSPECT Quant. J Nucl Med. 2019;60:50–59.
    OpenUrlAbstract/FREE Full Text
  4. 4.↵
    1. Hutton BF,
    2. Osiecki A
    . Correction of partial volume effects in myocardial SPECT. J Nucl Cardiol. 1998;5:402–413.
    OpenUrlCrossRefPubMed
  5. 5.↵
    1. Erlandsson K,
    2. Buvat I,
    3. Pretorius PH,
    4. Thomas BA,
    5. Hutton BF
    . A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys Med Biol. 2012;57:R119–R159.
    OpenUrlCrossRefPubMed
  6. 6.↵
    1. Tsui BM,
    2. Frey EC,
    3. Zhao X,
    4. Lalush DS,
    5. Johnston RE,
    6. McCartney WH
    . The importance and implementation of accurate 3D compensation methods for quantitative SPECT. Phys Med Biol. 1994;39:509–530.
    OpenUrlCrossRefPubMed
  7. 7.↵
    1. Yang J,
    2. Huang SC,
    3. Mega M,
    4. et al
    . Investigation of partial volume correction methods for brain FDG PET studies. IEEE Trans Nucl Sci. 1996;43:3322–3327.
    OpenUrlCrossRef
  8. 8.↵
    1. Jackson P,
    2. Hardcastle N,
    3. Dawe N,
    4. Kron T,
    5. Hofman MS,
    6. Hicks RJ
    . Deep learning renal segmentation for fully automated radiation dose estimation in unsealed source therapy. Front Oncol. 2018;8:215.
    OpenUrl
  9. 9.↵
    1. Chen Y,
    2. Goorden MC,
    3. Beekman FJ
    . Automatic attenuation map estimation from SPECT data only for brain perfusion scans using convolutional neural networks. Phys Med Biol. 2021;66:065006.
    OpenUrl
  10. 10.↵
    1. Rydén T,
    2. Van Essen M,
    3. Marin I,
    4. Svensson J,
    5. Bernhardt P
    . Deep-learning generation of synthetic intermediate projections improves 177Lu SPECT images reconstructed with sparsely acquired projections. J Nucl Med. 2021;62:528–535.
    OpenUrlAbstract/FREE Full Text
  11. 11.↵
    1. Leube J,
    2. Gustafsson J,
    3. Lassmann M,
    4. Salas-Ramirez M,
    5. Tran-Gia J
    . Analysis of a deep learning-based method for generation of SPECT projections based on a large Monte Carlo simulated dataset. EJNMMI Phys. 2022;9:47.
  12. 12.↵
    1. Liu J,
    2. Yang Y,
    3. Wernick MN,
    4. Pretorius PH,
    5. King MA
    . Deep learning with noise-to-noise training for denoising in SPECT myocardial perfusion imaging. Med Phys. 2021;48:156–168.
    OpenUrl
  13. 13.↵
    1. Xie H,
    2. Liu Z,
    3. Shi L,
    4. et al
    . Segmentation-free PVC for cardiac SPECT using a densely-connected multi-dimensional dynamic network. IEEE Trans Med Imaging. 2023;42:1325–1336.
    OpenUrl
  14. 14.↵
    1. Li Z,
    2. Fessler JA,
    3. Mikell JK,
    4. Wilderman SJ,
    5. Dewaraja YK
    . DblurDoseNet: a deep residual learning network for voxel radionuclide dosimetry compensating for single-photon emission computerized tomography imaging resolution. Med Phys. 2022;49:1216–1230.
    OpenUrl
  15. 15.↵
    1. Begum NJ,
    2. Glatting G,
    3. Wester HJ,
    4. Eiber M,
    5. Beer AJ,
    6. Kletting P
    . The effect of ligand amount, affinity and internalization on PSMA-targeted imaging and therapy: a simulation study using a PBPK model. Sci Rep. 2019;9:20041.
    OpenUrl
  16. 16.↵
    1. Ljungberg M,
    2. Strand SE
    . A Monte-Carlo program for the simulation of scintillation camera characteristics. Comput Methods Programs Biomed. 1989;29:257–272.
    OpenUrlCrossRefPubMed
  17. 17.↵
    1. Thielemans K,
    2. Tsoumpas C,
    3. Mustafovic S,
    4. et al
    . STIR: software for tomographic image reconstruction release 2. Phys Med Biol. 2012;57:867–883.
    OpenUrlCrossRefPubMed
  18. 18.↵
    1. Merlin T,
    2. Stute S,
    3. Benoit D,
    4. et al
    . CASToR: a generic data organization and processing code framework for multi-modal and multi-dimensional tomographic reconstruction. Phys Med Biol. 2018;63:185005.
  19. 19.↵
    1. Segars WP,
    2. Sturgeon G,
    3. Mendonca S,
    4. Grimes J,
    5. Tsui BMW
    . 4D XCAT phantom for multimodality imaging research. Med Phys. 2010;37:4902–4915.
    OpenUrlCrossRefPubMed
  20. 20.↵
    1. Ronneberger O,
    2. Fischer P,
    3. Brox T
    . U-Net: convolutional networks for biomedical image segmentation. arXiv website. https://arxiv.org/abs/1505.04597. Published May 18, 2015. Accessed March 25, 2024.
  21. 21.↵
    1. Zbontar J,
    2. Knoll F,
    3. Sriram A,
    4. et al
    . fastMRI: an open dataset and benchmarks for accelerated MRI. arXiv website. https://arxiv.org/abs/1811.08839. Published November 21, 2018. Accessed March 25, 2024.
  22. 22.↵
    1. Paszke A,
    2. Gross S,
    3. Massa F,
    4. et al
    . PyTorch: an imperative style, high-performance deep learning library. arXiv website. https://arxiv.org/abs/1912.01703. Published December 3, 2019. Accessed March 25, 2024.
  23. 23.↵
    1. Kingma DP,
    2. Ba J
    . Adam: a method for stochastic optimization. arXiv website. https://arxiv.org/abs/1412.6980. Published December 22, 2014. Accessed March 25, 2024.
  24. 24.↵
    1. Alom MZ,
    2. Hasan M,
    3. Yakopcic C,
    4. Taha T,
    5. Asari V
    . Recurrent residual convolutional neural network based on U-Net (R2U-Net) for medical image segmentation. arXiv website. https://arxiv.org/abs/1802.06955. Published February 20, 2018. Accessed March 25, 2024.
  25. 25.↵
    1. Oktay O,
    2. Schlemper J,
    3. Folgoc L,
    4. et al
    . Attention U-Net: learning where to look for the pancreas. arXiv website. https://arxiv.org/abs/1804.03999. Published April 11, 2018. Accessed March 25, 2024.
  26. 26.↵
    1. Su R,
    2. Liu H
    1. Wang Y,
    2. He Z,
    3. Xie P,
    4. et al
    . Segment medical image using U-Net combining recurrent residuals and attention. In: Su R, Liu H, eds. Medical Imaging and Computer-Aided Diagnosis . Springer; 2020:77–86.
  27. 27.↵
    1. Zhou Z,
    2. Rahman Siddiquee MM,
    3. Tajbakhsh N,
    4. Liang J
    . UNet++: a nested U-Net architecture for medical image segmentation. arXiv website. https://arxiv.org/abs/1807.10165. Published July 18, 2018. Accessed March 25, 2024.
  28. 28.↵
    1. Wang Z,
    2. Bovik AC,
    3. Sheikh HR,
    4. Simoncelli EP
    . Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13:600–612.
    OpenUrlCrossRefPubMed
  29. 29.↵
    1. Thomas BA,
    2. Cuplov V,
    3. Bousse A,
    4. et al
    . PETPVC: a toolbox for performing partial volume correction techniques in positron emission tomography. Phys Med Biol. 2016;61:7975–7993.
    OpenUrlCrossRef
  30. 30.↵
    1. Tran-Gia J,
    2. Lassmann M
    . Optimizing image quantification for 177Lu SPECT/CT based on a 3D printed 2-compartment kidney phantom. J Nucl Med. 2018;59:616–624.
    OpenUrlAbstract/FREE Full Text
  31. 31.↵
    1. Tran-Gia J,
    2. Denis-Bacelar AM,
    3. Ferreira KM,
    4. et al
    . A multicentre and multi-national evaluation of the accuracy of quantitative Lu-177 SPECT/CT imaging performed within the MRTDosimetry project. EJNMMI Phys. 2021;8:55.
    OpenUrl
  32. 32.↵
    1. Rinscheid A,
    2. Kletting P,
    3. Eiber M,
    4. Beer AJ,
    5. Glatting G
    . Influence of sampling schedules on [177Lu]Lu-PSMA dosimetry. EJNMMI Phys. 2020;7:41.
    OpenUrl
  • Received for publication October 27, 2023.
  • Revision received March 15, 2024.
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Keywords